Polynomial Regression

Polynomial Regression is a type of regression analysis where the relationship between the independent variable x and the dependent variable y is modeled as an nth degree polynomial. It allows us to fit a non-linear curve to the data, which is useful when the relationship between the variables is not linear.

📘 Description:

Polynomial regression fits a curve to the data using this general formula:

y = β0 + β1x + β2x2 + β3x3 + ⋯ + βnxn + ε

Where:

• y is the target variable (e.g., Salary)
• x is the feature (e.g., Level)
• β_i are the coefficients
• n is the degree of the polynomial

📁 Dataset: polynomial.csv

Assume the CSV contains:

Level	Salary
1	45000
2	50000
3	60000
4	80000
5	110000
6	150000
7	200000
8	300000
9	500000
10	1000000

🧠 Why Use Polynomial Regression?

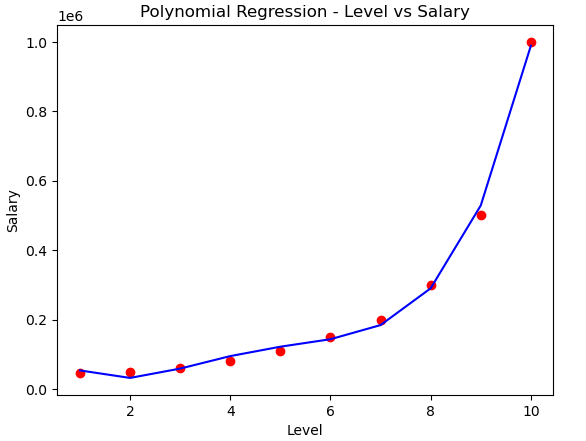
Linear regression would underfit this data (Salary doesn't grow linearly with Level). Polynomial regression can model the exponential-like increase more accurately.

🧪 Example: Polynomial Regression

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
from sklearn.preprocessing import PolynomialFeatures

# Load data
dataset = pd.read_csv('polynomial.csv')
X = dataset[['Level']]  # Feature
y = dataset['Salary']   # Target

# Create polynomial features (degree 4)
poly_features = PolynomialFeatures(degree=4)
X_poly = poly_features.fit_transform(X)

# Train polynomial regression model
model = LinearRegression()
model.fit(X_poly, y)

# Use DataFrame instead of raw NumPy array
level_df =  pd.DataFrame({'Level': [6.5]})
level_poly = poly_features.transform(level_df)
predicted_salary = model.predict(level_poly)

print(f"Predicted salary for level 6.5: ${predicted_salary[0]:,.2f}")

# Plot
plt.scatter(X, y, color='red')
plt.plot(X, model.predict(X_poly), color='blue')
plt.title("Polynomial Regression - Level vs Salary")
plt.xlabel("Level")
plt.ylabel("Salary")
plt.show()

Output:
A smooth curve fitting the dataset points much better than a straight line.
Predicted salary for level 6.5: $158,862.45